数据结构与算法

发表于 | 分类于
字数统计 5058
简单介绍数据结构和算法，以代码示例的方式加以解释和说明。

1. 算法概述

1.1. 什么是算法？

  • 通俗的讲，算法是指解决问题的一种方法或一个过程。更严格地讲，算法是右若干条指令组成的有穷序列。
  • 程序与算法不同，程序是算法用某种程序设计语言的具体实现。

1.2. 算法的复杂性

算法复杂性的高低体现在运行该算法所需要的计算机资源的多少上。

2. 数据结构和算法目录

首先明确一点：程序=数据结构+算法
Table 1: 数据结构和算法表
线性结构 树 堆 图 排序算法
数组、单链表和双链表 二叉查找树 二叉堆 图的理论基础 冒泡排序
Linux内核中双向链表的经典实现 AVL树 左倾堆 无向图 快速排序
栈 伸展树 斜堆 有向图 插入排序
队列 红黑树 二项堆 深度优先搜索和广度优先搜索 希尔排序
  哈夫曼树 斐波那契堆 拓扑排序 选择排序
  … … Kruskal算法 堆排序
      Prim算法 归并排序
      Dijkstra算法 桶排序
      … 基数排序
        …

3. 线性结构

常用的线性结构有：线性表，栈，队列，循环队列，数组。
  • 线性表：是一种线性结构，它是具有相同类型的n(n≥0)个数据元素组成的有限序列。
    • 顺序表：是在计算机内存中以数组的形式保存的线性表，是指用一组地址连续的存储单元依次存储数据元素的线性结构。
    • 链表（Linked list）
      • 单链表：它由节点组成，每个节点都包含下一个节点的指针。
        • 单链表分为：
          • 动态单链表
          • 静态单链表

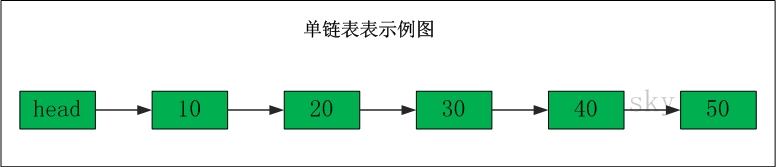
        • 单链表操作图示 linked-list-01.jpg 

          表头为空，表头的后继节点是"节点10"，"节点10"的后继节点是"节点20"。

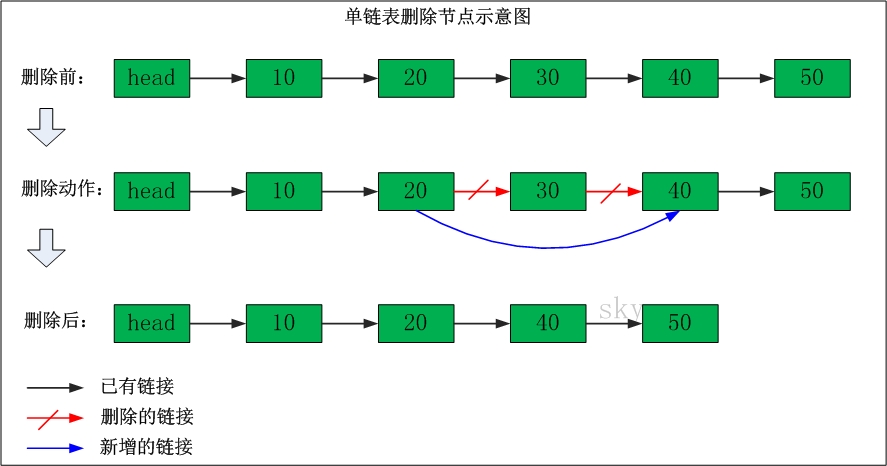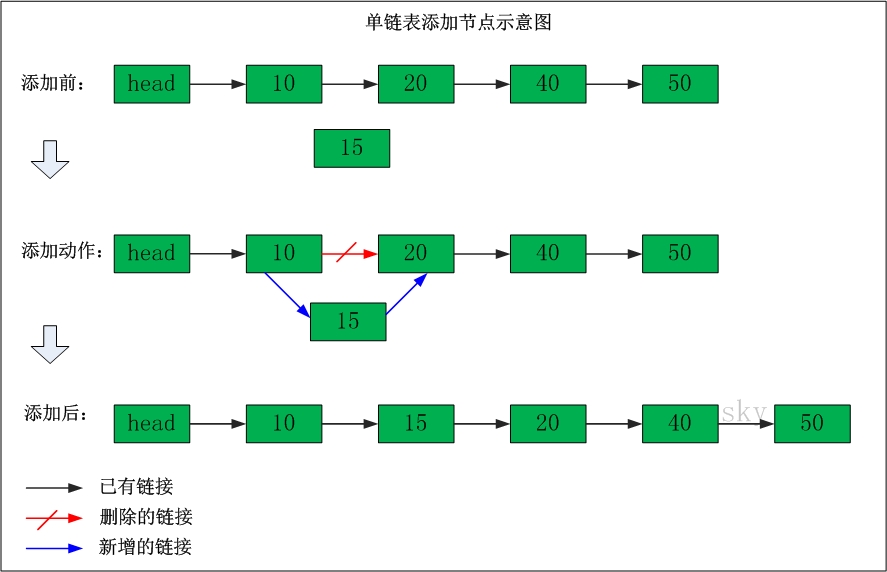
          删除节点 linked-list-02.jpg 添加节点 linked-list-03.jpg

        • 单链表的特点是：节点的链接方向是单向的；相对于数组来说，单链表的的随机访问速度较慢，但是单链表删除/添加数据的效率很高。
      • 双链表：它也是由节点组成，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。

        • 双链表操作图示 linked-list-04.jpg 

          表头为空，表头的后继节点为"节点10"(数据为10的节点)；"节点10"的后继节点是"节点20"(数据为10的节点)，"节点20"的前继节点是"节点10"；"节点20"的后继节点是"节点30"，"节点30"的前继节点是"节点20"；...；末尾节点的后继节点是表头。

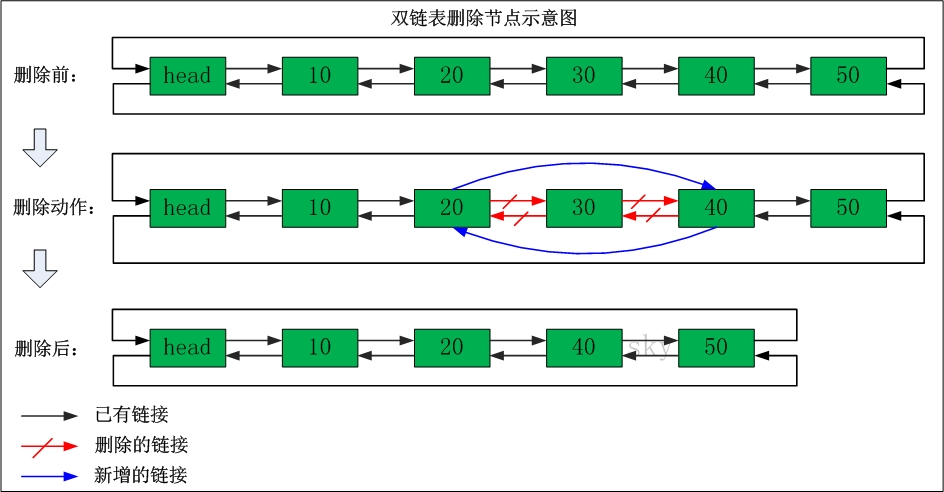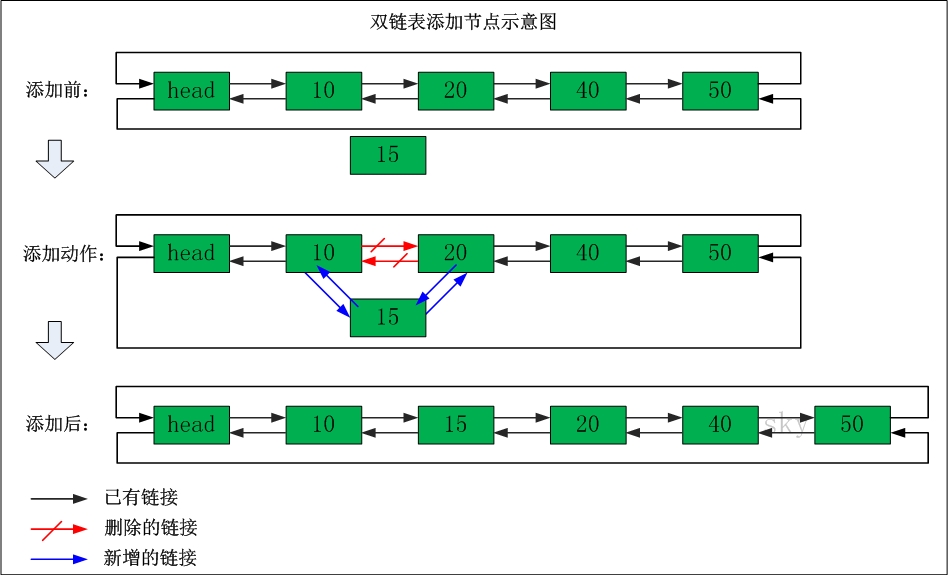
          删除节点 linked-list-05.jpg 添加节点 linked-list-06.jpg

        • 代码实现

          • Java 

            /**
 * Java 实现的双向链表。 
 * 注：java自带的集合包中有实现双向链表，路径是:java.util.LinkedList
 */
public class DoubleLink<T>
      • 循环链表
        • 单循环链表
        • 双循环链表
  • 栈（stack）：是计算机科学中一种特殊的串列形式的抽象数据类型，按照后进先出（LIFO, Last In First Out）的原理运作。其特殊之处在于只能允许在链表或数组的一端（称为堆栈顶端指针，英语：top）进行加入数据（英语：push）和输出数据（英语：pop）的运算。
  • 队列：又称为伫列（queue），是先进先出（FIFO, First-In-First-Out）的线性表。队列只允许在后端（称为rear）进行插入操作，在前端（称为front）进行删除操作。
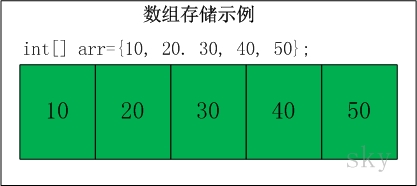
  • 数组：在计算机科学中，数组数据结构（英语：array data structure），简称数组（英语：Array），是由相同类型的元素（element）的集合所组成的数据结构，分配一块连续的内存来存储。 array-data-structure-01.jpg
    • 数组的特点是：数据的元素在上下界内是连续的；随机访问速度快。

4. 树

4.1. 二叉树

4.2. AVL 树

4.3. 伸展树

4.4. 红黑树

4.5. 哈夫曼树

5. 堆

6. 图

7. 排序算法

7.1. 冒泡排序(BubbleSort)

7.1.1. 介绍(Introduction)

en 

Bubblesort is a popular,but inefficient,sorting algorithm. It works by repeatedly swapping adjacent elements that are out of order.

cn 

冒泡排序是一种较简单的排序算法。它会遍历若干次要排序的数列，每次遍历时，它都会从前往后依次的比较相邻两个数的大小；如果前者比后者大，
则交换它们的位置。这样，一次遍历之后，最大的元素就在数列的末尾！ 采用相同的方法再次遍历时，第二大的元素就被排列在最大元素之前。重复
此操作，直到整个数列都有序为止！

7.1.2. 伪代码(pseudo code)

for i = 1 to A.length - 1
    for j = A:length downto i + 1
        if A[j] < A[j-1]   
            exchange A[j] with A[j - 1]

7.1.3. 时间复杂度和稳定性

冒泡排序的时间复杂度是O(N2)。
假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢？N-1次！因此，冒泡排序的时间复杂度是O(N2)。

冒泡排序是稳定的算法，它满足稳定算法的定义。
算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

7.1.4. 实现(realization)

C 

int i,j;
int flag; // 标记
for (i=n-1; i>0; i--)
{
    flag = 0; // 初始化标记为0
    // 将a[0...i]中最大的数据放在末尾
    for (j=0; j<i; j++)
    {
        if (a[j] > a[j+1])
        {
            swap(a[j], a[j+1]);
            flag = 1;    // 若发生交换，则设标记为1
        }
    }
    if (flag==0)
        break;// 若没发生交换，则说明数列已有序。
}

C# 

//Core code.
for (int i = 0; i < arrInt.Length - 1; i++)
{
    for (int j = 1; j < arrInt.Length - i; j++)
    {
        if (arrInt[j] < arrInt[j - 1])
        {
            //交换值
            int temp = arrInt[j];
            arrInt[j] = arrInt[j - 1];
            arrInt[j - 1] = temp;
        }
    }
}

Java 

public static void BubbleSort(int[] arr,int num) {
    for (int i = 0; i < arr.length; i++) {
            for (int j = num-1; j >i; j--) {
                    if (arr[i]>arr[j]) {
                            int temp=arr[i];
                            arr[i]=arr[j];
                            arr[j]=temp;
                    }
            }
    }
    for(int k=0;k<num;k++){
            System.out.print(arr[k]+" ");
    }
}

PHP 

function BubbleSort($arr){
        for($i=0;$i<count($arr);$i++){
                for($j=0;$j<$i;$j++){
                        if($arr[$i]>$arr[$j]){
                                $temp = $arr[$i];
                                $arr[$i] = $arr[$j];
                                $arr[$j] = $temp;
                        }
                }
        }
        foreach($arr as $value){
                echo $value." ";
        }
}

7.2. 快速排序(QuickSort)

7.2.1. 介绍(Introduction)

cn 

快速排序(Quick Sort)使用分治法策略。
基本思想是：选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分；其中一部分的所有数据都比另外
一部分的所有数据都要小。然后，再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此
达到整个数据变成有序序列。

快速排序流程：
(1) 从数列中挑出一个基准值。
(2) 将所有比基准值小的摆放在基准前面，所有比基准值大的摆在基准的后面(相同的数可以到任一边)；在这个分区退出之后，该基准就处于数列的中间位置。
(3) 递归地把"基准值前面的子数列"和"基准值后面的子数列"进行排序。

7.2.2. 伪代码(pseudo code)

7.2.3. 时间复杂度和稳定

快速排序的时间复杂度在最坏情况下是O(N2)，平均的时间复杂度是O(N*lgN)。 
这句话很好理解：假设被排序的数列中有N个数。遍历一次的时间复杂度是O(N)，需要遍历多少次呢？至少lg(N+1)次，最多N次。
(01) 为什么最少是lg(N+1)次？快速排序是采用的分治法进行遍历的，我们将它看作一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的定义，它的深度至少是lg(N+1)。因此，快速排序的遍历次数最少是lg(N+1)次。
(02) 为什么最多是N次？这个应该非常简单，还是将快速排序看作一棵二叉树，它的深度最大是N。因此，快读排序的遍历次数最多是N次。

快速排序是不稳定的算法，它不满足稳定算法的定义。

7.2.4. 实现(realization)

C 

/**
* arr -- 待排序的数组
* left -- 数组的左边界
* right -- 数组的右边界
*/
void quick_sort(int arr[],int left,int right){
    if(left < right){
            int i,j,k;
            i = left;
            j = right;
            k = arr[i];
            while(i < j){
                    while(i < j && arr[j] > k){
                            j--; // 从右往左找一个小于 k 的数
                    }
                    if(i < j){
                            arr[i++] = arr[j];
                    }
                    while(i<j && arr[i] < k){
                            i++; // 从左往右找第一个大于 k 的数
                    }
            }
            arr[i] = k;
            quick_sort(arr,left,i-1);
            quick_sort(arr,i+1,right);
    }
}

Java 






PHP

















7.3. 插入排序(InsertSort)








7.3.1. 介绍(Instoduction)






7.3.2. 伪代码(pseudo code)






for j=2 to A.length
    key=A[j];
    //Insert A[j] into the sorted sequence A[1..j-1]
    i=j-1
    while i>0 and A[i]>key
         A[i+1]=A[i]
         i=i-1
    A[i+1]=key











7.3.3. 实现(realization)














7.3.4. 分而治之(divideand-conquer)


















7.4. 选择排序






7.5. 希尔排序






7.6. 归并排序






7.7. 基数排序






7.8. 堆排序









9. 附录A 伪代码





伪代码(Pseudocode)是一种算法描述语言。使用伪代码的目的是为了使被描述的算法可以容易地以任何一种编程语言(C, Java, Pascal)实现。







9.1. 语法规则








9.1.1. 变量的声明





算法中出现的数组、变量可以是以下类型：整数、实数、字符、字符串或指针。









9.1.2. 指令的表示





在算法中的某些指令或子任务可以用文字来叙述，例如，”设x是A中的最大项”，这里A是一个数组；或者”将x插入L中”，这里L是一个链表。这样做的目的是为了避免因那些与主要问题无关的细节使算法本身杂乱无章。









9.1.3. 表达式





算术表达式可以使用通常的算术运算符（+，-，*，/，以及表示幂的^）。逻辑表达式可以使用关系运算符 = 、≠、<、>、≤ 和 ≥，以及逻辑运算符与(and)、或（or）、非（not）。









9.1.4. 赋值语句





赋值语句是如下形式的语句：a←b。这里a是变量、数组项，b是算术表达式、逻辑表达式或指针表达式。语句的含义是将b的值赋给a。


变量交换：若a和b都是变量、数组项，那么记号a<->b 表示a和b的内容进行交换。









9.1.5. goto语句




goto label（goto标号）









9.1.6. 分支结构






if i=10
    then xxxx
    else xxxx //else 和 then 要对齐

//或者
if i=10
    then xxxx //if 后面必定跟上then，else后面不用跟then
    elseif i=9 //elseif 要连在一起写
        then xxxx
        yyyy
    else  xxxx //else 跟在 elseif 的 then 对齐











9.1.7. 循环结构






// while
while time<10
    do  xxxxx //while后面必定要紧跟缩进的do
    xxxxx
end

// for
for var init to limit by incr 
        do s
end
// 这里var是变量，init、limit和incr都是算术表达式，而s是由一个或多个语句组成的语句串。初始时，var被赋予init的值。假若incr≥0，则只要var≤limit，就执行s并且将incr加到var上。（假若incr<0，则只要var≥limit，就执行s并且将incr加到var上）。incr的符号不能由s来该改变。











9.1.8. 程序的结束





exit语句可以在通常的结束条件满足之前，被用来结束while循环或者for循环的执行。


return用来指出一个算法执行的终点









9.1.9. 注释风格





算法中的注释被括在 * * 之中。









9.1.10. 函数的编写





函数的伪代码格式例子为：search（A，name）， 参数类型可以不给出，但必须在注释中说明。











9.2. 实例





伪代码：





x ← 0
y ← 0
z ← 0

while x < N
do x ← x + 1
y ← x + y
for t ← 0 to 10
do z ← ( z + x * y ) / 100
repeat
y ← y + 1
z ← z - y
until z < 0
z ← x * y

y ← y / 2







C 语言代码：





#inlude <stdio.h>
int x, y, z = 0;
int N=10;

while( z < N )
{
    x++;
    y += x;
  　for(int t = 0; t < 10; t++ )
    {
        z = ( z + x * y ) / 100;
        do 
        {
          y ++;
          z -= y;
        } while( z >= 0 );
    }
    z = x * y;
}

y /= 2;